论文的思路是先介绍分块压缩感知BCS,然后介绍使用投影和硬阈值方法的迭代投影方法PL,接着将PL与维纳滤波器结合形成SPL(平滑PL),并且介绍了稀疏表示的几种基,提出了两种效果较好的稀疏基:CT与DDWT,并且将PL中的硬阈值用bivariate shrinkage(双变量收缩)代替。
BCS+SPL(PL+维纳滤波平滑)+CT or DDWT
首先介绍PL的框架,是赋予一些初值,通过迭代来逼近最优解。

其中γ为尺度因子,使用了ΦTΦ中最大的特征值,τ(i)是每次迭代中设定的门限值,CS中运用PL在一定程度上降低了计算复杂度,并且PL算法可以灵活的增加所需要的迭代停止条件。
论文的第三部分介绍了将BCS与SPL结合的框架:
3.1 BCS
BCS即图像分块压缩感知,将图像分成多个大小为B×B的图像块,设xj为每块的列向量表示,对每一个图像块采用观测矩阵ΦB来测量。则每个图像块所对应得到的观测向量为yj=ΦBxj,其中ΦB是MB×B2的正交测量矩阵,并且有MB=[M/N]B2。
使用分块压缩感知有以下几个好处:首先由于分块后观测矩阵ΦB的尺寸变小,降低了所需的存储空间;其次,在编码端不需要等到整幅图像都完成观测后再进行编码,能在图像块投影到观测矩阵后就进行编码传输;最后算法中初始化使用的x(0)是根据最小均方误差来计算的,分块后的图像由于观测矩阵尺寸变小了,所以计算复杂度随之降低,在算法中,我们选用图像分块的尺寸大小B为32。
3.2 SPL
PL迭代算法中结合维纳滤波器能消除由于分块压缩感知导致的重构图像中的块效应,论文中SPL的迭代过程如下所示:

其中维纳滤波器的窗口大小为3×3,在算法中的初始化和迭代停止条件如下图所示,下文会对其中的阈值继续进行讨论。

论文的第四部分主要介绍了稀疏基和阈值:
4.1 Transforms
在图像压缩感知中,DWT被广泛应用于将信号进行稀疏表示,但是离散小波变换缺少移不变特性和方向选择性。据此提出了两种方向变换:轮廓波变换(CT)以及复值离散小波变换(complex-valued DWTs),复值离散小波变化使用了二元树DWT, 称为双树复小波变换DDWT。
4.2 阈值
SPL中应用是是硬阈值方法,论文中提出了一种通用的门限方法,如下所示:

其中λ是控制收敛的常数因子,K是变换系数的数目,σ(i)是采用一个鲁邦的中值滤波器来估计的: 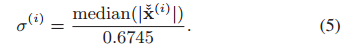
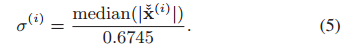
硬阈值本质上假定了系数之间是互相独立的,但对于所采用的方向变换,双变量收缩在变换系数和他们各自的父系数之间采用了统计依赖关系,能达到比硬阈值更好的效果,论文中所采用的方法如下图所示:

参考文献:
[1] Mun S,Fowler J E.Block compressed sensing of images using directional transforms[C]//Image Processing(ICIP),2009 IEEE International Conference on.IEEE,2009:3021-3024